Als het gaat omantennesDe vraag die mensen het meest bezighoudt is: "Hoe wordt straling eigenlijk bereikt?" Hoe plant het elektromagnetische veld dat door de signaalbron wordt gegenereerd zich voort door de transmissielijn en in de antenne, en hoe "scheidt" het zich uiteindelijk van de antenne om een vrije ruimtegolf te vormen?
1. Enkeldraads straling
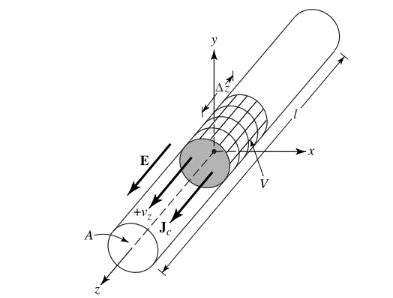
Laten we aannemen dat de ladingsdichtheid, uitgedrukt als qv (Coulomb/m³), uniform verdeeld is in een cirkelvormige draad met een dwarsdoorsnedeoppervlakte van a en een volume van V, zoals weergegeven in Figuur 1.
Figuur 1
De totale lading Q in volume V beweegt in de z-richting met een constante snelheid Vz (m/s). Hieruit kan worden afgeleid dat de stroomdichtheid Jz op de dwarsdoorsnede van de draad gelijk is aan:
Jz = qv vz (1)
Als de draad een ideale geleider is, is de stroomdichtheid Js aan het draadoppervlak:
Js = qs vz (2)
Waarbij qs de oppervlakteladingsdichtheid is. Als de draad erg dun is (idealiter is de straal 0), kan de stroom in de draad als volgt worden uitgedrukt:
Iz = ql vz (3)
Waarbij ql (coulomb/meter) de lading per lengte-eenheid is.
We houden ons voornamelijk bezig met dunne draden, en de conclusies zijn van toepassing op de bovenstaande drie gevallen. Als de stroom in de tijd varieert, is de afgeleide van formule (3) met betrekking tot de tijd als volgt:
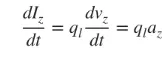
(4)
az is de ladingsversnelling. Als de draadlengte l is, kan (4) als volgt worden geschreven:
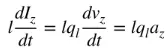
(5)
Vergelijking (5) beschrijft de basisrelatie tussen stroom en lading, en tevens de basisrelatie van elektromagnetische straling. Simpel gezegd, om straling te produceren, moet er een tijdsafhankelijke stroom of versnelling (of vertraging) van de lading zijn. We hebben het meestal over stroom in tijdsafhankelijke toepassingen, terwijl lading het vaakst wordt genoemd in transiënte toepassingen. Om ladingversnelling (of -vertraging) te produceren, moet de draad gebogen, gevouwen en onderbroken zijn. Wanneer de lading oscilleert in een tijdsafhankelijke beweging, zal dit ook periodieke ladingversnelling (of -vertraging) of een tijdsafhankelijke stroom produceren. Daarom:
1) Als de lading niet beweegt, is er geen stroom en geen straling.
2) Als de lading met een constante snelheid beweegt:
a. Als de draad recht en oneindig lang is, is er geen straling.
b. Als de draad gebogen, gevouwen of onderbroken is, zoals weergegeven in figuur 2, is er sprake van straling.
3) Als de lading in de loop van de tijd oscilleert, zal de lading uitstralen, zelfs als de draad recht is.
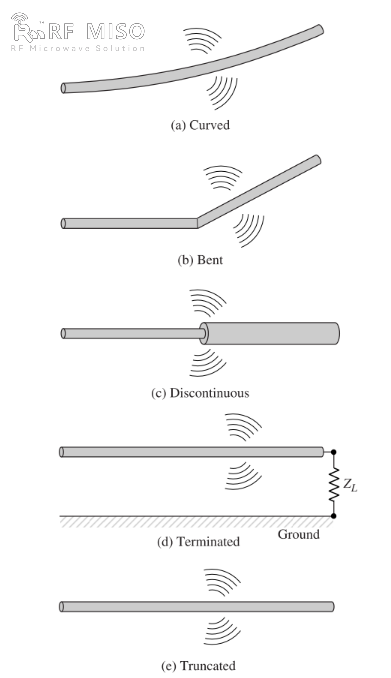
Figuur 2
Een kwalitatief begrip van het stralingsmechanisme kan worden verkregen door te kijken naar een gepulseerde bron die is aangesloten op een open draad die via een belasting aan het open uiteinde kan worden geaard, zoals weergegeven in figuur 2(d). Wanneer de draad aanvankelijk onder spanning wordt gezet, worden de ladingen (vrije elektronen) in de draad in beweging gebracht door de elektrische veldlijnen die door de bron worden gegenereerd. Terwijl de ladingen aan het uiteinde van de draad waar de bron zich bevindt, worden versneld en vervolgens worden afgeremd (negatieve versnelling ten opzichte van de oorspronkelijke beweging) wanneer ze aan het uiteinde worden gereflecteerd, ontstaat er een stralingsveld aan de uiteinden en langs de rest van de draad. De versnelling van de ladingen wordt bewerkstelligd door een externe krachtbron die de ladingen in beweging zet en het bijbehorende stralingsveld produceert. De afremming van de ladingen aan de uiteinden van de draad wordt bewerkstelligd door interne krachten die samenhangen met het geïnduceerde veld, dat wordt veroorzaakt door de accumulatie van geconcentreerde ladingen aan de uiteinden van de draad. De interne krachten verkrijgen energie door de accumulatie van lading naarmate de snelheid ervan afneemt tot nul aan de uiteinden van de draad. De versnelling van de ladingen als gevolg van de elektrische veldopwekking en de vertraging van de ladingen als gevolg van de discontinuïteit of vloeiende curve van de draadimpedantie zijn dus de mechanismen voor het genereren van elektromagnetische straling. Hoewel zowel stroomdichtheid (Jc) als ladingsdichtheid (qv) brontermen zijn in de Maxwell-vergelijkingen, wordt lading beschouwd als een meer fundamentele grootheid, vooral voor transiënte velden. Hoewel deze verklaring van straling voornamelijk wordt gebruikt voor transiënte toestanden, kan ze ook worden gebruikt om stationaire straling te verklaren.
Ik beveel verschillende uitstekende producten aan.antenneproductengefabriceerd doorRFMISO:
2. Tweedraadsbestraling
Sluit een spanningsbron aan op een tweeaderige transmissielijn die verbonden is met een antenne, zoals weergegeven in figuur 3(a). Door spanning op de tweeaderige lijn aan te leggen, ontstaat er een elektrisch veld tussen de geleiders. De elektrische veldlijnen werken in op de vrije elektronen (die gemakkelijk van atomen loskomen) die met elke geleider verbonden zijn en dwingen ze in beweging te komen. De beweging van ladingen genereert stroom, die op zijn beurt een magnetisch veld opwekt.
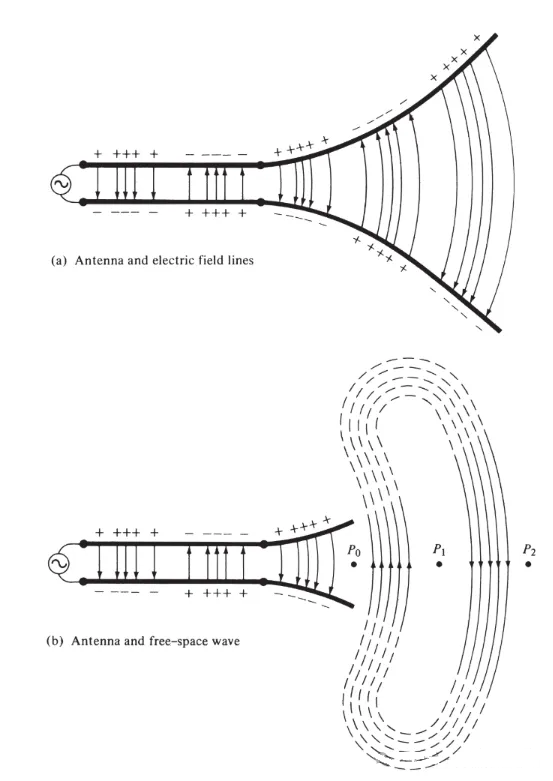
Figuur 3
We hebben geaccepteerd dat elektrische veldlijnen beginnen met positieve ladingen en eindigen met negatieve ladingen. Natuurlijk kunnen ze ook beginnen met positieve ladingen en eindigen in het oneindige; of beginnen in het oneindige en eindigen met negatieve ladingen; of gesloten lussen vormen die noch beginnen noch eindigen met ladingen. Magnetische veldlijnen vormen altijd gesloten lussen rond stroomvoerende geleiders, omdat er in de natuurkunde geen magnetische ladingen bestaan. In sommige wiskundige formules worden equivalente magnetische ladingen en magnetische stromen geïntroduceerd om de dualiteit tussen oplossingen met vermogen en magnetische bronnen aan te tonen.
De elektrische veldlijnen die tussen twee geleiders zijn getekend, helpen om de ladingsverdeling weer te geven. Als we aannemen dat de spanningsbron sinusvormig is, verwachten we dat het elektrische veld tussen de geleiders ook sinusvormig is met een periode gelijk aan die van de bron. De relatieve grootte van de elektrische veldsterkte wordt weergegeven door de dichtheid van de elektrische veldlijnen, en de pijlen geven de relatieve richting aan (positief of negatief). De opwekking van tijdsafhankelijke elektrische en magnetische velden tussen de geleiders vormt een elektromagnetische golf die zich voortplant langs de transmissielijn, zoals weergegeven in figuur 3(a). De elektromagnetische golf komt de antenne binnen met de lading en de bijbehorende stroom. Als we een deel van de antennestructuur verwijderen, zoals weergegeven in figuur 3(b), kan een vrije-ruimtegolf worden gevormd door de open uiteinden van de elektrische veldlijnen (aangegeven met de stippellijnen) met elkaar te "verbinden". De vrije-ruimtegolf is ook periodiek, maar het punt met constante fase P0 beweegt met de lichtsnelheid naar buiten en legt een afstand van λ/2 af (naar P1) in een halve periode. Vlakbij de antenne beweegt het constante-fasepunt P0 sneller dan de lichtsnelheid en nadert de lichtsnelheid op punten ver van de antenne. Figuur 4 toont de verdeling van het elektrische veld in vrije ruimte van de λ/2-antenne op t = 0, t/8, t/4 en 3T/8.
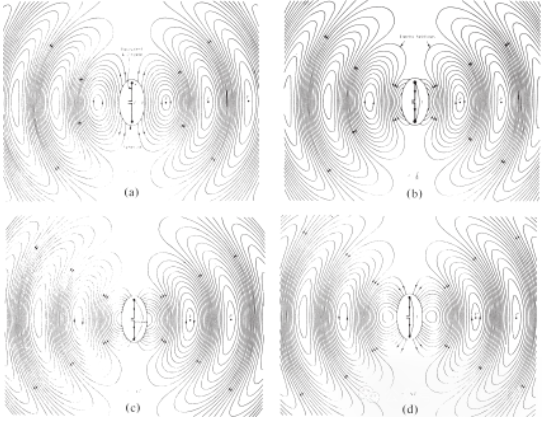
Figuur 4. Elektrische veldverdeling in vrije ruimte van de λ/2-antenne op t = 0, t/8, t/4 en 3T/8.
Het is niet bekend hoe de geleide golven zich van de antenne scheiden en uiteindelijk gevormd worden om zich in de vrije ruimte voort te planten. We kunnen geleide golven en golven in de vrije ruimte vergelijken met watergolven, die bijvoorbeeld kunnen ontstaan door een steen die in een kalm wateroppervlak wordt gegooid. Zodra de verstoring in het water begint, worden er watergolven gegenereerd die zich naar buiten verspreiden. Zelfs als de verstoring stopt, stoppen de golven niet, maar blijven ze zich voortplanten. Als de verstoring aanhoudt, worden er constant nieuwe golven gegenereerd en loopt de voortplanting van deze golven achter op die van de andere golven.
Hetzelfde geldt voor elektromagnetische golven die worden gegenereerd door elektrische storingen. Als de initiële elektrische storing van de bron van korte duur is, planten de gegenereerde elektromagnetische golven zich voort in de transmissielijn, komen ze de antenne binnen en stralen ze uiteindelijk uit als vrije ruimtegolven, zelfs als de excitatie niet langer aanwezig is (net zoals watergolven en de verstoring die ze veroorzaken). Als de elektrische storing continu is, bestaan de elektromagnetische golven continu en volgen ze deze op de voet tijdens de voortplanting, zoals te zien is in de biconische antenne in figuur 5. Wanneer elektromagnetische golven zich in transmissielijnen en antennes bevinden, is hun bestaan gerelateerd aan de aanwezigheid van elektrische lading in de geleider. Wanneer de golven echter worden uitgestraald, vormen ze een gesloten lus en is er geen lading meer nodig om hun bestaan in stand te houden. Dit leidt ons tot de conclusie dat:
Het opwekken van het veld vereist versnelling en vertraging van de lading, maar het in stand houden van het veld vereist geen versnelling en vertraging van de lading.
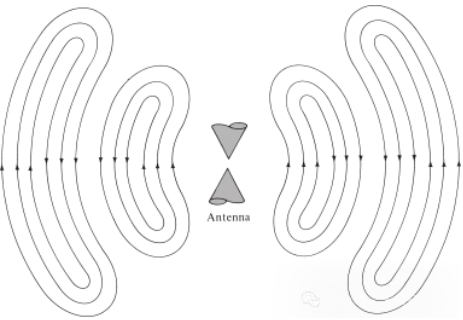
Figuur 5
3. Dipoolstraling
We proberen het mechanisme te verklaren waarmee de elektrische veldlijnen zich van de antenne losmaken en vrije-ruimtegolven vormen, en nemen de dipoolantenne als voorbeeld. Hoewel het een vereenvoudigde uitleg is, maakt het de generatie van vrije-ruimtegolven wel intuïtief zichtbaar. Figuur 6(a) toont de elektrische veldlijnen die tussen de twee armen van de dipool ontstaan wanneer de elektrische veldlijnen in het eerste kwart van de cyclus λ/4 naar buiten bewegen. Laten we voor dit voorbeeld aannemen dat er 3 elektrische veldlijnen worden gevormd. In het volgende kwart van de cyclus bewegen de oorspronkelijke drie elektrische veldlijnen nog eens λ/4 (in totaal λ/2 vanaf het beginpunt), en de ladingsdichtheid op de geleider begint af te nemen. Dit kan worden beschouwd als het ontstaan door de introductie van tegengestelde ladingen, die de ladingen op de geleider aan het einde van de eerste helft van de cyclus opheffen. De door de tegengestelde ladingen gegenereerde elektrische veldlijnen zijn er 3 en bewegen een afstand van λ/4, wat wordt weergegeven door de stippellijnen in figuur 6(b).
Het eindresultaat is dat er drie neerwaartse elektrische veldlijnen zijn in de eerste λ/4-afstand en hetzelfde aantal opwaartse elektrische veldlijnen in de tweede λ/4-afstand. Omdat er geen netto lading op de antenne aanwezig is, moeten de elektrische veldlijnen zich van de geleider scheiden en samenkomen om een gesloten lus te vormen. Dit wordt weergegeven in figuur 6(c). In de tweede helft wordt hetzelfde fysische proces gevolgd, maar let op: de richting is tegengesteld. Daarna wordt het proces herhaald en gaat het oneindig door, waardoor een elektrische veldverdeling ontstaat die vergelijkbaar is met figuur 4.
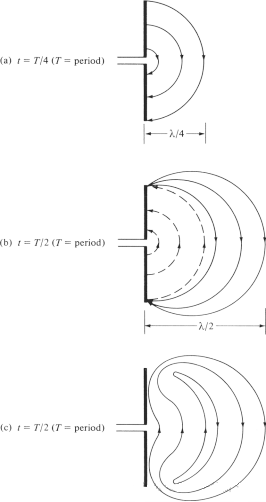
Figuur 6
Ga voor meer informatie over antennes naar:
Geplaatst op: 20 juni 2024










